%load ../../rapaio-bootstrap.ipynb
Adding dependency io.github.padreati:rapaio-lib:7.0.1
Solving dependencies
Resolved artifacts count: 1
Add to classpath: /home/ati/work/rapaio-jupyter-kernel/target/mima_cache/io/github/padreati/rapaio-lib/7.0.1/rapaio-lib-7.0.1.jar
Built-in Data sets#
For learning purposes some well-known data sets are already incorporated into rapaio library. All built in data sets are available via rapaio.datasets.Datasets class. This is an utility class which provides some standard data sets used in many statistical and machine learning text books. Some of them are described below
Iris data set#
The Iris flower data set or Fisher’s Iris data set is a multivariate data set introduced by Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis. It is sometimes called Anderson’s Iris data set because Edgar Anderson collected the data to quantify the morphological variation of Iris flowers of three related species.
Two of the three species were collected in the Gaspé Peninsula all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus.
The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). There are for measures for each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.
var iris = Datasets.loadIrisDataset();
iris.printSummary();
Frame Summary
=============
* rowCount: 150
* complete: 150/150
* varCount: 5
* varNames:
0. sepal-length : dbl | 3. petal-width : dbl |
1. sepal-width : dbl | 4. class : nom |
2. petal-length : dbl |
* summary:
sepal-length [dbl] sepal-width [dbl] petal-length [dbl] petal-width [dbl]
Min. : 4.3000000 Min. : 2.0000000 Min. : 1.0000000 Min. : 0.1000000
1st Qu. : 5.1000000 1st Qu. : 2.8000000 1st Qu. : 1.6000000 1st Qu. : 0.3000000
Median : 5.8000000 Median : 3.0000000 Median : 4.3500000 Median : 1.3000000
Mean : 5.8433333 Mean : 3.0573333 Mean : 3.7580000 Mean : 1.1993333
2nd Qu. : 6.4000000 2nd Qu. : 3.3000000 2nd Qu. : 5.1000000 2nd Qu. : 1.8000000
Max. : 7.9000000 Max. : 4.4000000 Max. : 6.9000000 Max. : 2.5000000
class [nom]
versicolor : 50
setosa : 50
virginica : 50
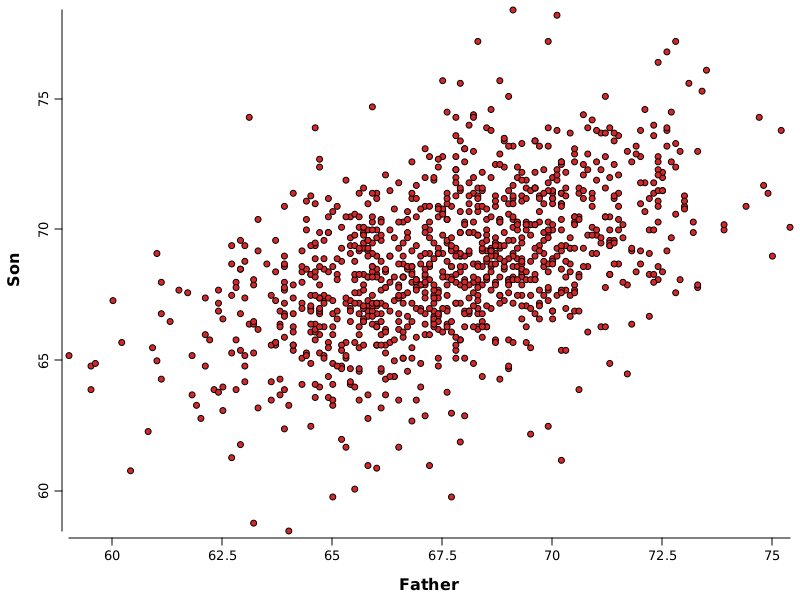
Pearson’s Height Data#
This simple data set comes from a famous experiment by Karl Pearson around 1903. The number of cases is 1078. The original data values were rounded to produce heights to the nearest \(0.1\) inch.
var df = Datasets.loadPearsonHeightDataset();
df.printSummary();
Frame Summary
=============
* rowCount: 1078
* complete: 1078/1078
* varCount: 2
* varNames:
0. Father : dbl |
1. Son : dbl |
* summary:
Father [dbl] Son [dbl] Mean : 67.6868275 Mean : 68.6842301
Min. : 59.0000000 Min. : 58.5000000 2nd Qu. : 69.6000000 2nd Qu. : 70.5000000
1st Qu. : 65.8000000 1st Qu. : 66.9000000 Max. : 75.4000000 Max. : 78.4000000
Median : 67.8000000 Median : 68.6000000
WS.image(points(df.rvar("Father"), df.rvar("Son"), pch.circleFull(), fill(1)));
Advertising data set#
This data set is one of the first data sets used in Introduction to Statistical Learning book to illustrate various topics for linear regression. It contains observations which relates sales as an assumed result of advertising into various types of media communication like TV, radio or newspapers.
var df = Datasets.loadISLAdvertising()
df.printSummary()
Frame Summary
=============
* rowCount: 200
* complete: 200/200
* varCount: 4
* varNames:
0. TV : dbl |
1. Radio : dbl |
2. Newspaper : dbl |
3. Sales : dbl |
* summary:
TV [dbl] Radio [dbl] Newspaper [dbl] Sales [dbl]
Min. : 0.7000000 Min. : 0.0000000 Min. : 0.3000000 Min. : 1.6000000
1st Qu. : 74.3750000 1st Qu. : 9.9750000 1st Qu. : 12.7500000 1st Qu. : 10.3750000
Median : 149.7500000 Median : 22.9000000 Median : 25.7500000 Median : 12.9000000
Mean : 147.0425000 Mean : 23.2640000 Mean : 30.5540000 Mean : 14.0225000
2nd Qu. : 218.8250000 2nd Qu. : 36.5250000 2nd Qu. : 45.1000000 2nd Qu. : 17.4000000
Max. : 296.4000000 Max. : 49.6000000 Max. : 114.0000000 Max. : 27.0000000
